A sparse matrix or sparse array is a matrix in which most of the elements are zero. A sparse matrix contains very few non-zero elements.
A sparse matrix can be represented using
1. Triplet representation
2. Linked representation.
1. Triplet representation
Representing a sparse matrix by an array leads to wastage of lots of memory as zeroes in the matrix are of no use in most of the cases. So, instead of storing zeroes, store only non-zero elements. This means storing non-zero elements with triples- (Row, Column, value).
Consider 3x3 matrix:
The triplet representation of given matrix is:
|
Rows |
Columns |
Values |
|
3 |
3 |
2 |
|
0 |
2 |
4 |
|
1 |
1 |
5 |
2. Linked representation.
Using linked list for representing a sparse matrix allows faster execution of operations like insertions and deletions.
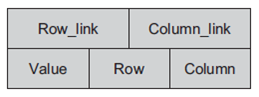
The node structure of a linked sparse matrix is
The value, row and column fields contain data value, row index and column index respectively. The fields row_link and column_link are pointers to the next element in a circular list containing matrix elements for row and column, respectively.
The principle is that all the nodes, particularly in a row (or column), are circularly linked with each other; each row and column contains a header node. Thus, for a sparse matrix of order m x n, we have to maintain m header nodes for all rows and n header nodes for all columns, plus one extra node, the header node.
Header is one additional header node that points to the starting address of the sparse matrix. It represents:
1. Row field contains the number of rows.
2. Column field contains the total number of non-zero entries.
3. Row_link field contains pointer to the header node of the first row.
4. Column_link field contains pointer to the header node of the first column.
Header nodes for each row and column are used such that more efficient insertion and deletion algorithms can be implemented. The header node of each row contains 0 in the column field, and that of each column contains 0 in the row field.





No comments:
Post a Comment