Priority Queue

A priority queue is a collection of elements where the elements are stored according to their priority levels.

The order in which the elements should be removed is decided by the priority of the element.

Rules to be followed to maintain a priority queue:

1. The element with a higher priority is processed before any element of lower priority.

2. If there were elements with the same priority, then the element added first in the queue would get processed first.

Priority queues are used for implementing job scheduling by the operating system where jobs with higher priority are to be processed first.

Another application of priority queues is in simulation systems where the priority corresponds to event times.

There are two ways to implement priority queues:

Method 1:

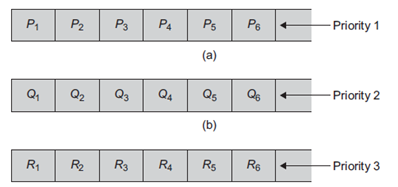
Using separate queues for each priority and following FIFO (First In First Out) behavior.

 

Jobs are always removed from the front of the queue. The elements in the second queue are removed only when the first queue is empty, and the elements from the third queue are removed only when the second queue is empty, and so on.

 

Method 2:

Priority queue is implemented by using a structure for a queue.

typedef struct

{

int Data;

int priority;

};

 

 

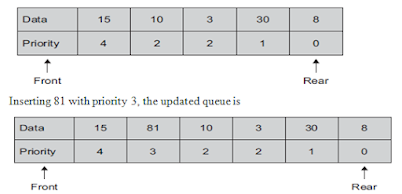
The highest priority element is at the front and that of the lowest priority is at the rear. When an element is to be deleted, it behaves as a normal queue, the element at front, which has the highest priority, is deleted first.

The two ways to implement a priority queue are sorted list and unsorted list.

Using sorted implementation deletion is easy (delete from beginning of list) but insertion is hard (find proper location of element). A linked list is convenient for this implementation.

Using unsorted implementation insertion is easy (add element at end) but deletion is hard (find highest priority element). An array is convenient for this implementation. If any array is used to store elements of a priority queue, then insertion of elements to the queue would be easy, but deletion of elements would be difficult. This is because while inserting elements in the priority queue, they are not inserted in an order. As a result, deleting an element with the highest priority would require examining the entire array to search for such an element and an element in a queue can be deleted from the front end only.